[NeurlPS'21] Graphormer: Transformer在图结构数据上的应用

分享
#1

论文链接：https://arxiv.org/pdf/2106.05234.pdf
代码仓库：GitHub - microsoft/Graphormer: Graphormer is a deep learning package that allows researchers and developers to train custom models for molecule modeling tasks. It aims to accelerate the research and application in AI for molecule science, such as material design, drug discovery, etc.

Introduction

为了得到更精确的分子性质，计算化学家们常使用基于量子力学力场的密度泛函理论 DFT （Density Functional Theory）预测，然而该方法非常耗时。若直接使用图神经网络 GNN 模型，输入分子的 2D 结构，则可以快速而准确地预测分子性质，并且在几秒钟内就能够完成。因此，目前图预测领域的主流算法主要是图神经网络（GNN）模型及其变种，比如图卷积网络（Graph Convolutional Net）、图注意力网络（Graph Attention Net）、图同构网络（Graph isomorphic Net）等。
但是，这些图神经网络的结构相对简单，表达能力有限，且经常会出现过度平滑（Over-Smoothing）的问题，即无法通过堆深网络而增加 GNN 的表达能力。为此，作者转变思路，希望可以在图预测学习任务中从图表达能力着手，来提升图预测性能。

Difficulty

经典的 Transformer 模型是处理序列类型数据的，如自然语言、语音等等，那么如何让这个模型处理图类型数据呢？最重要的是让 Transformer 学会编码图的结构信息。Transformer 的核心在于其自注意力机制，通过在计算中输入不同位置语义信息的相关性，可以捕捉到信息之间的关系，并且可基于这些关系得到对整个输入完整的表达（representation）。然而，自注意力机制无法捕捉到结构信息。对于自然语言序列而言，输入序列的结构信息可以简单认为是词与词的相对顺序，以及每个词在句子中的位置。对于图数据而言，这种结构信息更加复杂、多元，例如在图上的每个节点都有不同数量的邻居节点，两个节点之间可以有多种路径，每个边上都可能包含重要的信息。如何在图数据中成功应用 Transformer 的核心优势，最关键的难题是要确保模型可以正确利用这些图结构信息。

Structural Encoding

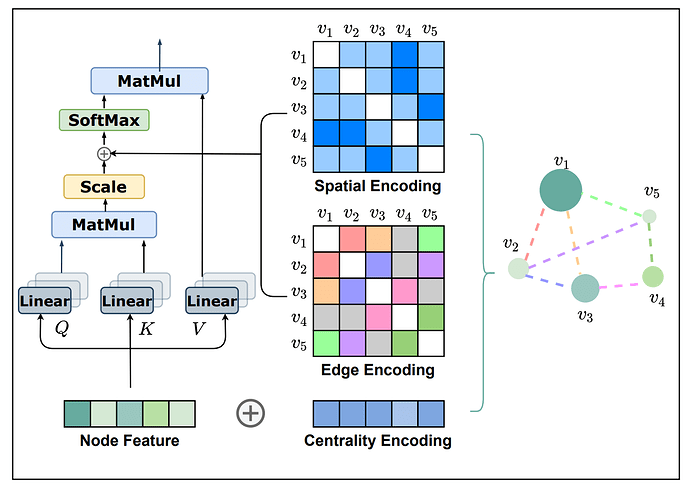
为了把 Transformer 模型强大的表达能力引入图结构数据中，作者提出了 Graphormer 模型。Graphormer 模型引入了三种结构编码，以帮助 Transformer 模型捕捉图的结构信息。这些结构编码让 Graphormer 模型的自注意力层可以成功捕捉到更“重要”的节点或节点对，从而令后续的注意力权重分配更准确。

1552×1109 105 KB

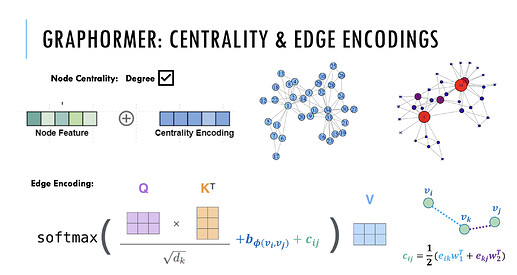
第一种编码，Centrality Encoding（中心性编码）。Centrality（中心性）是描述图中节点重要性的一个关键衡量指标。图的中心性有多种衡量方法，例如一个节点的“度”（degree）越大，代表这个节点与其他节点相连接的边越多，那么往往这样的节点就会更重要，如在疾病传播路线中的超级传播者，或社交网络上的大V、明星等。Centrality 还可以使用其他方法进行度量，如 Closeness、Betweenness、Page Rank 等。在 Graphormer 中，研究员们采用了最简单的度信息作为中心性编码，为模型引入节点重要性的信息。

具体地说，开发了一个中心性编码方法，它根据每个节点的度和出度给每个节点分配两个实值嵌入向量。当中心性编码应用于每个节点时，只需将其添加到节点特征中作为输入。

h_{i}^{(0)}=x_{i}+z_{\operatorname{deg}^{-}\left(v_{i}\right)}^{-}+z_{\operatorname{deg}^{+}\left(v_{i}\right)}^{+}

其中，𝑑z−,z+∈Rd 分别是由入度 deg−(vi) 和 出度 deg+⁡(vi) 指定的可学习的嵌入向量。对于无向图，deg−(vi) 和 deg+⁡(vi) 可以统一为 deg⁡(vi)。通过在输入中使用中心性编码，softmax attention 可以捕获 queries 和 keys 中的节点重要性信号。因此，该模型可以同时捕获注意机制中的语义相关性和节点的重要性。

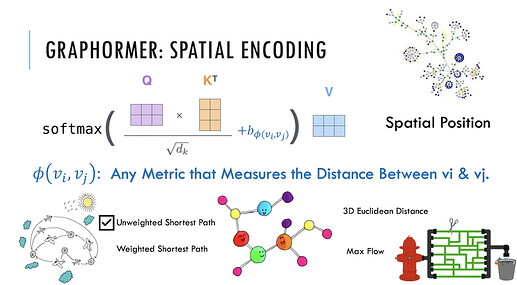
第二种编码，Spatial Encoding（空间编码）。实际上图结构信息不仅包含了每个节点上的重要性，也包含了节点之间的重要性。例如：邻居节点或距离相近的节点之间往往相关性比距离较远的节点相关性高。因此，研究员们为 Graphormer 设计了空间编码：给定一个合理的距离度量 ϕ(v_i, v_j), 根据两个节点(v_i, v_j)之间的距离，为其分配相应的编码向量。距离度量 ϕ(⋅) 的选择多种多样，对于一般性的图数据可以选择无权或带权的最短路径，而对于特别的图数据则可以有针对性的选择距离度量，例如物流节点之间的最大流量，化学分子 3D 结构中原子之间的欧氏距离等等。为了不失一般性，Graphormer 在实验中采取了无权的最短路径作为空间编码的距离度量。

具体地说，对于任何图 G，定义函数ϕ(vi,vj):V×V→R 测量 vi 和 vj 之间的空间关系。函数 ϕ 可通过图中节点之间的连通性来定义。在本文中，对于连通节点 vi 和 vj ， ϕ(vi,vj) 定义为 vi 和 vj 之间的最短路径(SPD)的距离。如果 vi 和 vj 不连通，将 𝜙ϕ 设置为一个特殊的值，即 −1−1。本文对给每对连通节点分配一个可学习的标量，将作为自注意模块中的一个偏差项。 Aij 表示为 Query-Key 乘积矩阵 A 的(i，j) 元素，因此有：

A_{i j}=\frac{\left(h_{i} W_{Q}\right)\left(h_{j} W_{K}\right)^{T}}{\sqrt{d}}+b_{\phi\left(v_{i}, v_{j}\right)}
其中，bϕ(vi,vj) 是一个由 ϕ(vi,vj) 索引的可学习的标量，并在所有层中共享。

对比于 GNNs，好处是：

    • 首先，GNNs 的感受域局限于邻居，而在 图中所涉及的范围是全局信息，每个节点可以关注其他节点；
    • 其次，通过使用 bϕ(vi,vj) ，单个 Transformer 层中的每个节点都可以根据图的结构信息自适应地关注所有其他节点。如果 bϕ(vi,vj) 是相对于 ϕ(vi,vj) 的递减函数，对于每个节点，模型可能会更关注其附近的节点，而对远离它较少的节点。

Screen Shot 2022-07-25 at 2.08.54 PM
Screen Shot 2022-07-25 at 2.08.54 PM1500×827 172 KB

第三种编码，Edge Encoding（边信息编码）。对于很多的图任务，连边上的信息有非常重要的作用，例如连边上的距离、流量等等。然而为处理序列数据而设计的 Transformer 模型并不具备捕捉连边上的信息的能力，因为序列数据中并不存在“连边”的概念。因此，作者设计了边信息编码，将连边上的信息作为权重偏置（Bias）引入注意力机制中。具体来说，在计算两个节点之间的相关性时，研究员们对这两个节点最短路径上的连边特征进行加权求和作为注意力偏置，其中权重是可学习的。

Screen Shot 2022-07-25 at 2.09.04 PM
Screen Shot 2022-07-25 at 2.09.04 PM2982×1588 333 KB

How Powerful is Graphormer?

Graphormer 可以表示 AGGREGATE 和 COMBINE 操作。

Fact 1. By choosing proper weights and distance function ϕ , the Graphormer layer can represent AGGREGATE and COMBINE steps of popular GNN models such as GIN, GCN, GraphSAGE.

该事实说明：

      1. Spatial encoding 使自注意模块能够区分节点 vi 的邻域集 N(vi)，从而使 softmax 函数能够计算出 N(vi) 上的平均统计量；
      1. 知道一个节点的程度，邻居的平均值可以转换为邻居的和；
      1. 通过 multiple heads 和 FFN， vi 和N(vi) 的表示可以分别处理，然后再组合在一起；

此外，进一步表明，通过使用空间编码，信号信号器可以超越经典的信息传递 GNNs，其表达能力不超过 1-WL 测试。

Connection between Self-attention and Virtual Node

除了比流行的 GNN 具有更好的表达性外，作者还发现在使用自注意和虚拟节点启发式之间存在着有趣的联系。如 OGB[22] 的排行榜所示，虚拟节点技巧在图中增加了连接到现有图中的所有节点，可以显著提高现有 GNN 的性能。从概念上讲，虚拟节点的好处是它可以聚合整个图的信息（比如 READOUT ），然后将其传播到每个节点。然而，在图中简单地添加一个超节点可能会导致信息传播的意外过度平滑。相反，这种图级的聚合和传播操作可以通过普通的自注意自然地实现，而不需要额外的编码。具体地说，可以证明以下事实：

Fact 2. By choosing proper weights, every node representation of the output of a Graphormer layer without additional encodings can represent MEAN READOUT functions.

这一事实利用了自我注意，每个节点可以注意所有其他节点。因此，它可以模拟图级读出(READOUT)操作，从整个图中聚合信息。除了理论上的论证外，作者还发现 Graphormer 没有遇到过度平滑的问题，这使得改进具有可扩展性。这一事实也激励了作者为图形读出引入一个特殊的节点。

Experiment

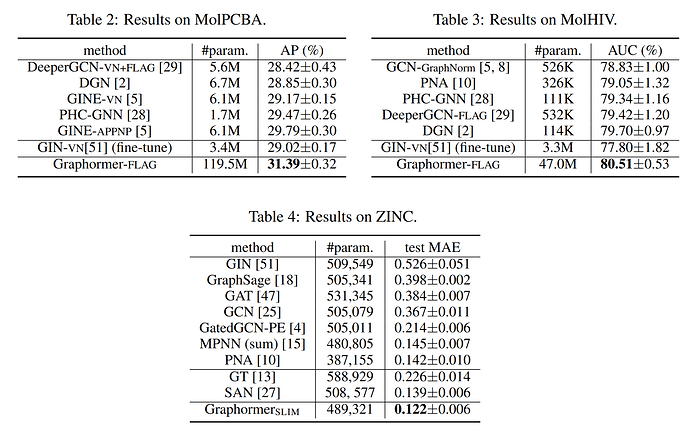
作者还在多个主流图预测任务排行榜上验证了 Graphormer 的效果。例如，OGB 数据集中的 ogbg-molhiv 任务（预测是否被 HIV 病毒感染），ogbg-molpcba 任务（预测分子的64种性质）以及 Benchmarking-GNN 数据集中的 ZINC 任务（对真实世界中存在的分子的受限溶解度 Constrained Solubility 进行预测）。Graphormer 均取得了优异的成绩，具体测试结果如下图：

2078×1309 343 KB

Conclusion

作者探讨了Transformer在图表示中的直接应用。通过三种新的图结构编码，所提出的Graphormer在广泛的流行的基准数据集上工作得非常好。虽然这些初步结果令人鼓舞，但仍存在许多挑战。例如，自注意模块的二次复杂度限制了在大图上的应用。通过在特定的图数据集上利用领域知识驱动的编码，可以预期提高性能。最后，提出了一种适用的图采样策略来提取节点表示。

Reference

1.论文解读（Graphormer）《Do Transformers Really Perform Bad for Graph Representation?》 - Learner- - 博客园
2.KDD Cup 2021 | 微软亚洲研究院Graphormer模型荣登OGB-LSC图预测赛道榜首

#2

A_{i j}=\frac{\left(h_{i} W_{Q}\right)\left(h_{j} W_{K}\right)^{T}}{\sqrt{d}}+b_{\phi\left(v_{i}, v_{j}\right)}