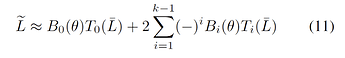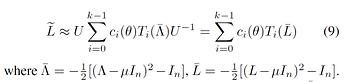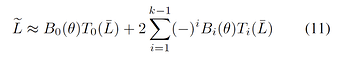前言
Hi 大家好,我是GNN课程的助教,本次优秀作业分享来自于课程学员程煜晴同学,在作业二中,她进行了许多的实验去对比不同NE算法的效果,并提供了详细的实验报告以及实验结果分析,对作业二有疑问的同学可以对她的作业进行参考。同时,我们也非常欢迎其他同学来踊跃分享自己高质量的作业,期待下一个分享的就是你。
1 选用数据集
from cogdl.datasets import build_dataset_from_name
dataset = build_dataset_from_name("ppi-ne")
graph = dataset[0]
print(graph)
labels = graph.y.numpy()
实验使用的是PPI数据集,这是一个蛋白质交互网络。其中每个节点代表一个蛋白质,每条边代表蛋白质之间的交互关系,节点标签代表蛋白质的某种状态。
该数据集共3890个样本点,50种标签,共76854条边。
2 实验设置
由于PPI数据集是一个多标签(multi-label)的数据集,所以需要训练一个多标签的线性分类器对每一维标签分别预测。
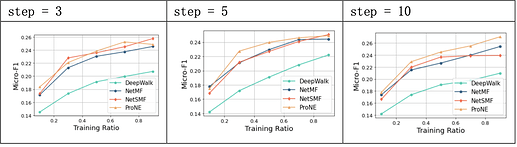
实验设置了5种不同的数据划分方式进行评估,其中训练集的比例分别为0.1~0.9。
使用Micro-F1指标作为最后的评估指标。
3 实验结果
3.1 DeepWalk
3.1.1 主要参数
- walk_length: 每个结点的游走长度;
- walk_num: 每个结点的游走次数;
- window_size: 窗口大小;
3.1.2 调参结果
默认值:
DeepWalk(dimension=128, walk_length=20, walk_num=10, window_size=7, worker=1, iteration=10)
3.1.3 结果分析
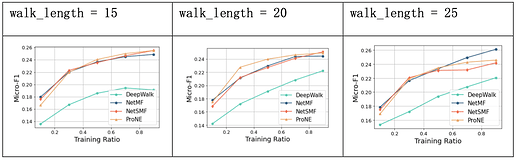
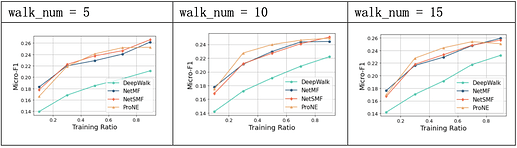
DeepWalk方法在图上进行随机路径采样,将采样得到的结点序列看做自然语言中的句子,之后利用语言建模中的SkipGram方法进行优化。
实验中,DeepWalk在PPI数据集上的预测精度相较其余三种较低,对比默认值发现, walk_length取20、walk_num取15、window_size取7时效果较好,游走长度更长、游走轮次更多次以及窗口值更大对模型的提升均有限。
3.2 NetMF
3.2.1 主要参数
- window_size: 窗口大小;
- rank: 特征对数;
- negative: 负采样结点数;
- is_large: 是否是大规模图,对应NetMF的不同计算方法:小图直接计算和分解Deepwalk metrix,大图通过特征分解做近似计算;
3.1.2 调参结果
默认值:
netmf = NetMF(dimension=128, window_size=5, rank=256, negative=5, is_large=False)
3.1.3 结果分析
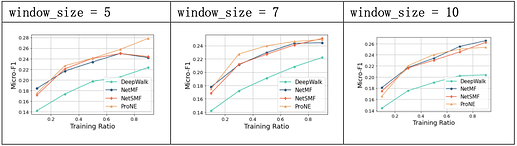
NetMF开辟了一种基于 SkipGram 和负采样的网络表示学习方法,实验中,NetMF方法在PPI数据集上,能够在训练集比例较小时就取得较好的效果。
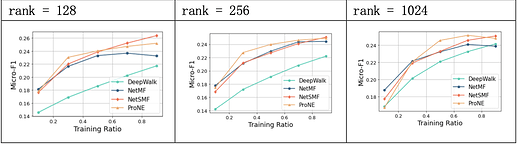
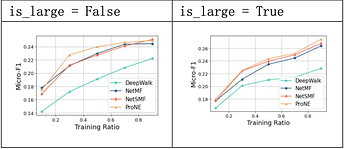
超参数window_size的值对模型效果有显著的影响;rank的值对于模型效果影响较小;is_large上,将数据作为大规模图处理的近似方法效果较好。
3.3 NetSMF
默认值:
netsmf = NetSMF(dimension=128, window_size=7, negative=1, num_round=100, worker=1)
3.3.1 主要参数
- window_size: 窗口大小;
- negative: 负采样结点数;
- num_round: 轮数;
3.3.2 调参结果
3.3.3 结果分析
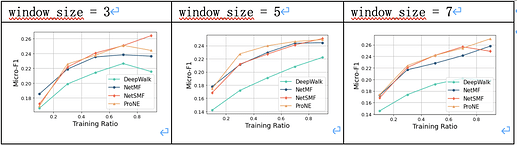
NetSMF将网络表示学习看做稀疏矩阵分解问题。
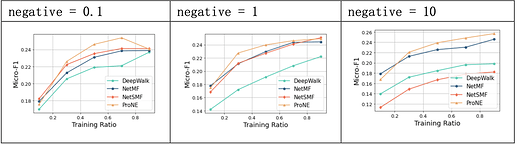
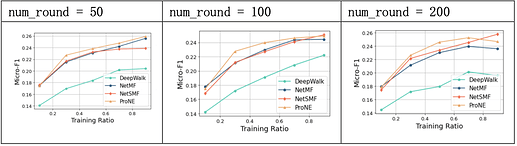
实验中,NetSMF方法在PPI数据集上的效果较好,与NetMF大致相当,对超参敏感,negative对于模型的影响较大;当num_round提升时,预测精度也有相应提升。
3.4 proNE
3.4.1 主要参数
-
step: 对应切比雪夫展开式中的 k 值;
-
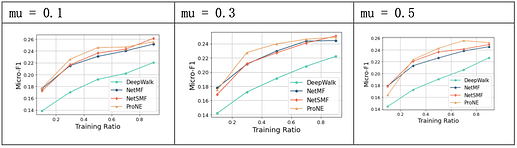
mu: 对应对角稀疏矩阵的参数 μ ;
-
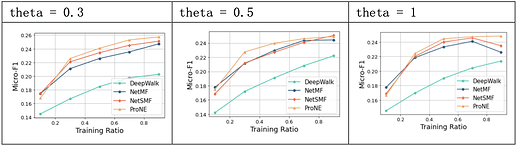
theta: 对应贝塞尔函数的参数 θ ;
3.4.2 调参结果
默认值:
prone = ProNE(dimension=128, step=50, mu=0.3, theta=0.5)
3.4.3 结果分析
proNE通过负采样方法构建一个稀疏矩阵进行分解,使得计算复杂度降低到 O(|V|d2+k|E|) ,并利用高阶Cheeger不等式对图的谱空间进行调制,让初始分解后得到的结点表示在谱空间进行传播。
proNE方法在PPI数据集上预测的效果较好,速度较快;当step取10时,模型效果较好,超参mu和theta相较step对模型效果影响较小。